№ 49. 1) Из точки А к окружности с центром О и радиусом R проведена касательная. Докажите, что точка С касания лежит на основании равнобедренного треугольника ОАВ, у которого ОА = АВ, ОВ = 2R. 2) Проведите касательную к окружности, проходящую через данную

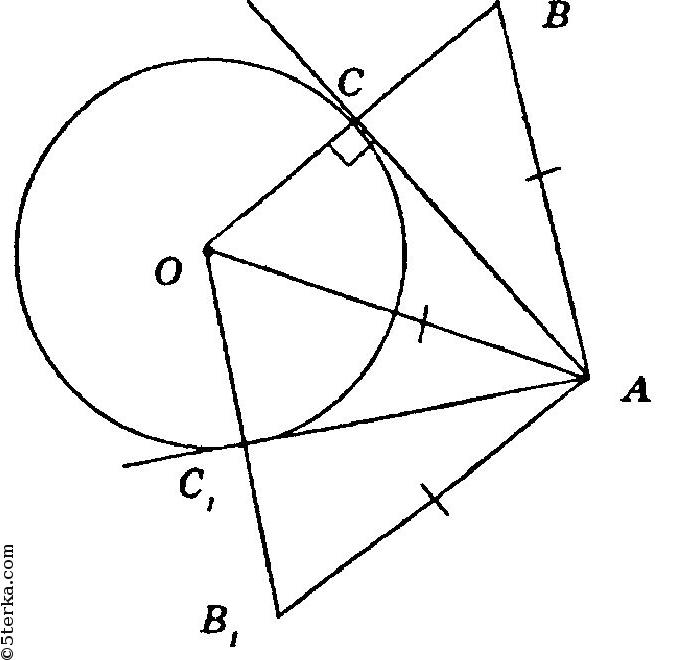
1) ОС ⊥ АС по определению. Продлим ОС до точки В так, что СВ = ОС. В ΔОВА отрезок АС является высотой и медианой, так как ОС = ВС по построению, таким образом, ΔОВА — равнобедренный. Откуда АО = АВ и ОВ = 2ОС = 2R.

2) Проведем к данной окружности касательную, проходящую через данную точку А. Сначала соединим точки О и А.

Затем проведем окружности с центром О и радиусом 2R и ОА. Они пересекаются в двух точках В и В₁.

ОВ и ОВ₁ пересекают окружность в точках С и С₁. Соединив их с точкой А, получим две касательные АС и АС₁.

ΔОАВ и ΔОАВ¹ — равнобедренные АС и АС₁ — медианы, значит они являются и высотами. Таким образом, АС ⊥ ОС = R, АС₁ ⊥ ОС₁ = R, следовательно, АС и АС₁ — касательные. Т.к. к окружности можно провести не более двух касательных (задача № 16 § 5), то построение закончено.