№ 37. Треугольники АВС и BAD равны, причем точки С и D лежат по разные стороны от прямой АВ. Докажите, что 1) треугольники CBD и DAC равны; 2) прямая CD делит отрезок АВ пополам.

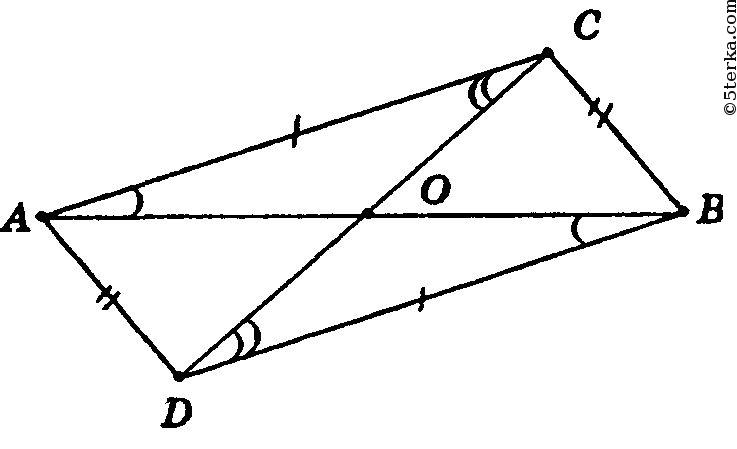
Т.к. ΔАВС = ΔABD, то АС = BD, CB = AD, ∠CAO = ∠OBD.

1) В ΔCBD и ΔDAC:

CD — общая

АС = DB, AD = CB (из условия).

Таким образом, ΔCBD = ΔDAC по 3-му признаку равенства треугольников, таким образом, ∠CDB = ∠DCA.

2) В ΔАОС и ΔDOB:

АС = BD, ∠CAO = ∠OBD, ∠CDB = ∠DCA.

Таким образом, ΔАОС = ΔDOB по 2-му признаку, откуда АО = ОВ. Следовательно, отрезок BD делит отрезок АВ пополам, что и требовалось доказать.