36. Даны четыре параллельные прямые. Докажите, что если какая-нибудь плоскость пересекает эти прямые в вершинах параллелограмма, то любая плоскость, не параллельная этим прямым, пересекает их в вершинах некоторого параллелограмма.

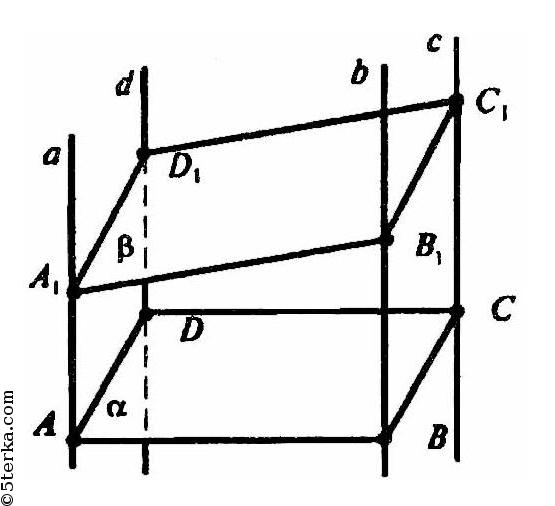
Пусть а, b, с, d — данные прямые, и плоскость α пересекает эти прямые в вершинах параллелограмма ABCD.

Пусть другая плоскость пересекает эти прямые в точках А₁, В₁, С₁, D₁ соответственно. плоскости αВВ₁А₁ и CDD₁C₁, параллельны, поскольку прямые АВ и CD, и прямые а и d параллельны. А, значит, плоскость β пересекает эти плоскости по параллельным прямым А₁В₁ и C₁D₁.

Аналогично устанавливается параллельность прямых В₁С₁ и Так что А₁В₁С₁В₁ — параллелограмм. Что и требовалось доказать.