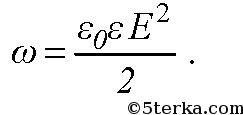Электрическое поле к задачнику по физике за 10-11 классы «Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.
Электрическое поле и электрический заряд — первичные понятия, которые не определяются аналогично понятиям точки и прямой в геометрии. Неподвижный заряд создает вокруг себя электрическое поле. Если замкнутая система обладала зарядом q, то при любых изменениях в ней заряд q сохраняется. Это фундаментальное утверждение носит название закона сохранения заряда.
Точечным зарядом называется заряд исчезающе малых размеров. Из эксперимента известно, что два точечных заряда q1 и q2 на расстоянии r взаимодействуют с силой F, значение которой определяется законом Кулона:
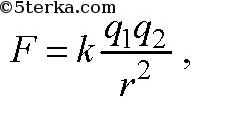
где

— коэффициент пропорциональности. Когда заряды одноименные, то они отталкиваются, когда разноименные — притягиваются.
Силовой характеристикой электрического поля является вектор напряженности E;. Рассмотрим некоторый заряд q, внесенный в электрическое поле E;. Тогда на него будет действовать сила F;, которая определяется формулой: F; = qE;. Это формула может служить определением вектора напряженности электрического поля. Для графического представления электростатического поля пользуются понятием линий напряженности. Эти линии начинаются на положительных зарядах и заканчиваются на отрицательных. Касательная в каждой точке линии напряженности направлена также, как и вектор E; . Если имеется N зарядов, каждый из которых создает свое поле E1;, E2;,…, EN; , то полная напряженность в любой точке пространства E; определяется как векторная сумма этих напряженностей (принцип суперпозиции):

Для точечного заряда q значение напряженности E в точке, удаленной от него на расстоянии r, выражается формулой:
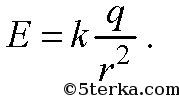
Проводником называется тело, содержащее свободные заряды. Если мы сообщим проводнику некоторый заряд q, то он распределится по поверхности, а внутри проводника поле будет равно нулю. Поверхностной плотностью о называется отношение заряда к площади поверхности проводника

Поле заряженного проводящего шара снаружи от него совпадает с полем точечного заряда, а внутри него равно нулю. Поле бесконечной заряженной проводящей плоскости с поверхностной плотностью заряда о определяется формулой:

где ε0 = 8,854⋅10-12 Ф/м — электрическая постоянная.
Диэлектриком называется тело, в котором отсутствуют свободные заряды. При помещении диэлектрика в электрическое поле происходит его поляризация, при этом поле E в диэлектрике уменьшается в ε раз:

где E0 — напряженность поля вне диэлектрика, ε — диэлектрическая проницаемость. При перемещении заряда q в электрическом поле E; на
расстояние
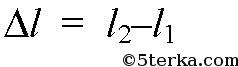
совершается работа A:
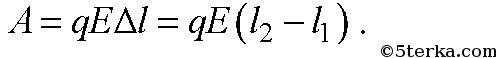
Изменение потенциальной энергии ΔWP равно:

Потенциал φ — энергетическая характеристика электрического поля, он определяется формулой:

Эквипотенциальные поверхности — это такие поверхности, в каждой точке которых потенциал постоянен. Потенциал поля φ в некоторой точке пространства, созданный N зарядами, равен алгебраической сумме потенциалов φ1, φ2,…, φN созданных отдельными зарядами (принцип суперпозиции): φ = φ1 + φ2 + … +
φN- Потенциал поля точечного заряда q на расстоянии r от него определяется формулой:

Напряжением U между точками A и B называется разность потенциалов:

где φ1 — потенциал в точке A, φ2 — потенциал в точке B. Напряжение U связано с напряженностью E электрического поля следующей формулой:

Конденсатором называется устройство, способное накапливать заряд. Емкость конденсатора C определяется как отношение заряда q на его обкладках к приложенному напряжению U:

Емкость не зависит от заряда и напряжения на нем, а определяется его геометрическими свойствами (формой и размером) и родом среды. Для плоского конденсатора емкость равна:

где ε — диэлектрическая проницаемость среды между обкладками, S — площадь обкладок, d — расстояние между обкладками. Энергия заряженного конденсатора W определяется формулой:

Плотность энергии ω электрического поля E выражается формулой: